Csonkolások, csillagok

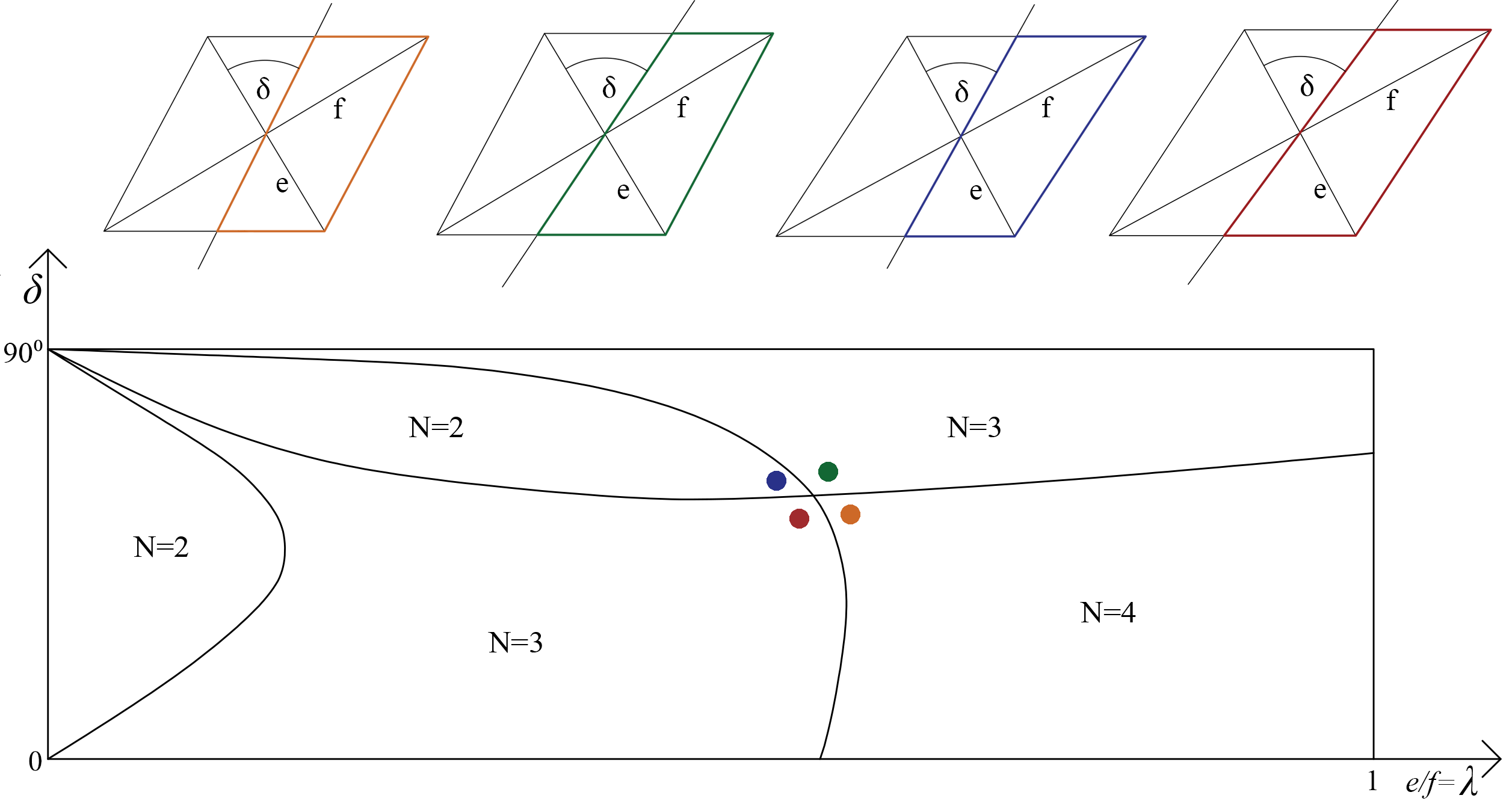
Dolgozatunkban egy egyparaméteres S(λ) síkidomcsaládot vágunk ketté súlypontján átmenő, egy meghatározott iránnyal δ szöget bezáró egyenessel. Az így keletkező S(λ,δ) síkidomokat merev testnek tekintve egyensúlyi helyzeteik N(λ,δ) számát vizsgáljuk λ és δ függvényében. A lehetséges kiindulási S(λ) síkidomok közül háromszögeket, téglalapokat, rombuszokat, szabályos sokszögeket valamint szabályos csillagokat vizsgálunk.

Az N(λ,δ) tehát egész értékű függvény. Azon (λ,δ) pontok, ahol a függvény értéke ugrik, görbéket határoznak meg a λ-δ síkon. Az így keletkezett görbék metszéspontjait elágazási-, vagy bifurkációs pontoknak nevezzük. Ezen pontokhoz, illetve ezen pontok kis környezetéhez tartozó síkidomok esetén a geometria végtelenül érzékennyé válik, alapvető statikai intuíciónk csődöt mond, ezért mérnöki, tervezői szemszögből fontos ezen különleges geometriájú idomok mélyebb megismerése.

A dolgozatunkban bemutatott egyensúly-elágazásokkal analóg jelenséggel találkoztunk mechanikai tanulmányainkban, amikor a rugalmas stabilitásvesztés jelenségét vizsgáltuk. Itt azt mutatjuk be, hogy matematikailag és mechanikailag is szorosan kapcsolódó jelenséggel ennél sokkal egyszerűbb feladatokban is találkozhatunk. Reményeink szerint ez közelebb vihet a rugalmas stabilitás jobb megértéséhez.

A dolgozatunkban bemutatott egyensúly-elágazások abban is segíthetnek, hogy közelebbről megérthessük a természetben zajló fizikai alakfejlődés folyamatait, melyek során hasonló jelenségek játszódnak le.

szerzők

• 
  Mándoki Réka
  építészmérnök
  nappali
• 
  Ther Péter Pál
  építészmérnök
  nappali
• 
  Tomasovszky Péter
  építészmérnök
  nappali

konzulens

• 
  Dr. Domokos Gábor
  egyetemi tanár, Morfológia és Geometriai Modellezés Tanszék