Alakevolúciós egyenlet használata membránfelületek számítására
A matematikában különböző felületek egzakt leírása, vizsgálata, illetve adott feltételeket kielégítő sima felületek létrehozása a differenciálgeometriai kutatások homlokterében áll. A rögzített peremű szappanhártya alakját megadó differenciálegyenletet J. L. Lagrange fedezte fel 1768-ban a klasszikus variációszámítás módszereinek kidolgozása folyamán, azonban tényleges megoldásokat csak a következő évtizedekben írtak le. G. Monge bizonyította, hogy a rögzített peremek közé kifeszíthető, minimális felülettel rendelkező sima felület átlaggörbülete minden pontjában zérus [1]. A minimálfelületek általánosításaként tekintsük azokat a felületeket, amelyekre minden pontban az átlaggörbület és a Gauss-féle szorzatgörbület ugyanazon lineáris összefüggést elégíti ki. Ezen felületeket J. Weingarten vizsgálta először a XIX. század közepén [2,3].
A dolgozatban egyrészről rámutatok arra, hogy a természetben megfigyelhető egyes kopási folyamatokat (pl.: folyómederben kopó szikla felülete) leíró egyirányú Bloore modell [4,5] stacionárius megoldásai Weingarten felületek, és megfelelő feltételek esetén a természeti formák közel Weingarten tulajdonságúak. Másrészről, ahogy a minimálfelületek a dominánsan feszített szerkezet alakjával állnak összefüggésben, úgy a Weingarten felületek is megfeleltethetőek adott terheket membrán feszültségekkel ellensúlyozó felületeknek. Azt találjuk tehát, hogy a természetben fellelhető formák membrán erőjátékú héjak geometriáját adják.
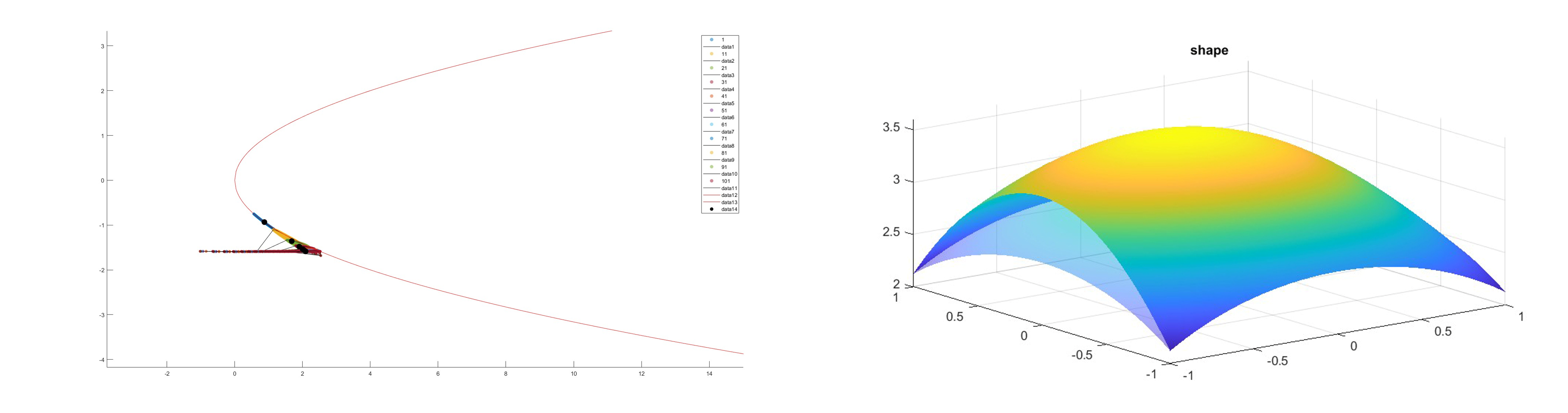
Kihasználva a fenti analógiát, dolgozatomban új formakeresési módszert mutatok be, mely evolúciós algoritmusként, a Bloore operátor szimulációjával állítja elő a minimálfelületet, illetve általános esetben a Weingarten felületet, rögzített Dirichlet peremek esetén. Rámutatok arra, hogy a téglalap alakú számítási tartomány esetén a Dirichlet peremek lehetnek inkompatibilisek a végső megoldással, ez a szerkezeti mechanikában a sarkok körül kialakuló ún. peremzavar matematikai magyarázata. A teljes, nemlineáris Bloore operátor szimulációja az erős nemlinearitás miatt nem minden esetben konvergens, azonban konvergencia esetén az elliptikus Monge-Ampère parciális differenciálegyenlet megoldását kapjuk eredményül.
[1] TH Colding and WP Minicozzi II. Minimal surfaces and mean curvature flow. arXiv preprint arXiv:1102.1411, 2011.
[2] J Weingarten. Ueber eine klasse auf einander abwickelbarer flächen. 1861.
[3] X Tellier, C Douthe, O Baverel, and L Hauswirth. Designing funicular grids with planar quads using isotropic linear-weingarten surfaces. International Journal of Solids and Structures, 264:112028, 2023.
[4] FJ Bloore. The shape of pebbles. Journal of the International Association for Mathematical Geology, 9:113-122, 1977.
[5] G Domokos, GW Gibbons, and AA Sipos. Circular, stationary profiles emerging in unidirectional abrasion. Mathematical Geosciences, 46:483491, 2014
szerző
-
Szondi Máté Álmos
Építészmérnöki mesterképzési szak osztatlan
egységes, osztatlan képzés

