Inhomogén politópok mechanikai komplexitása - avagy van-e egy tetraédernek lelke?

Politópnak nevezzük a d-dimenziós Euklideszi térben (d-k) dimenziós lineáris sokaságok ((k=0,1, ... (d-1)) által határolt alakzatokat. Poligonnak, vagy másnéven sokszögnek nevezzük a d=2 dimenziós politópokat és poliédernek nevezzük a d=3 dimenziós politópokat. Ebben a dolgozatban az utóbb felsorolt két esettel foglalkozunk.

Egy politóp konvex, ha két tetszőleges pontját összekötő szakasz a politóp belsejében marad. Inhomogén tömegeloszlást feltételezve egy politóp súlypontja annak belsejében bárhol lehet.

Poligonok statikai viselkedésének jellemzésére bevezetjük az egyensúlyi osztályozó vektor fogalmát mely egy N-szög esetén egy N dimenziós, bináris vektor, melynek k-adik eleme 1, ha létezik pontosan k darab stabil helyzettel rendelkező N-szög, egyébként az elem 0. Háromszögek és négyszögek esetében bebizonyítjuk, hogy a kombinatorikailag lehetséges 2^3 illetve 2^4 vektor közül geometriailag csak 2 illetve 5 darab realizálódhat és fel is soroljuk ezeket a vektorokat.

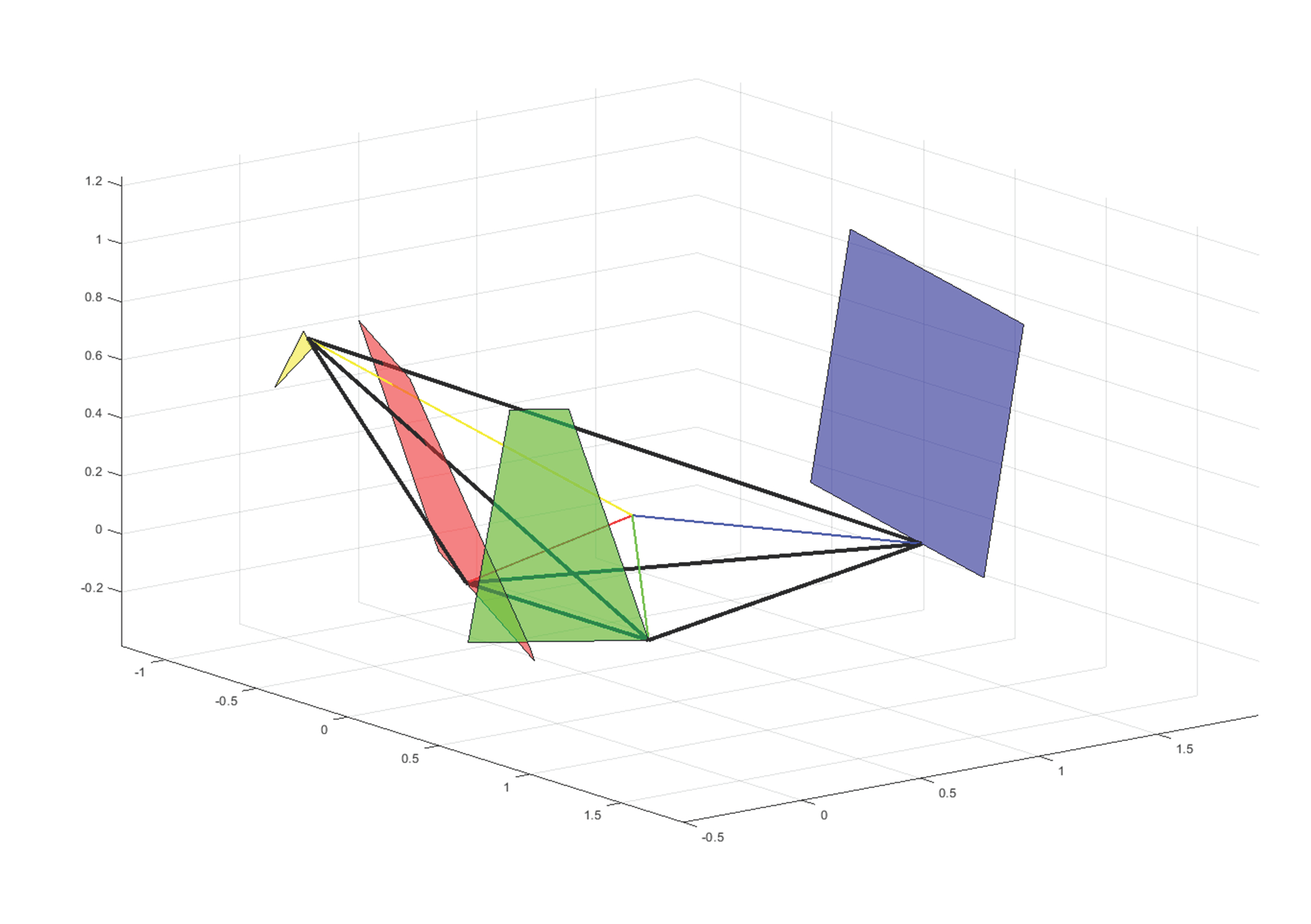
Poliéderek esetében bevezetjük az egyensúlyi osztályozó mátrix fogalmát, mely egy F lapú, V csúcsú poliéder esetén egy FxV méretű, bináris elemekből álló mátrix, melynek (i,j) eleme 1, ha létezik pontosan S=i, U=j stabil illetve instabil egyensúlyi helyzettel rendelkező F lapú, V csúcsú konvex poliéder, egyébként az elem 0.

MATLAB programban számított eredmények alapján sejtéseket fogalmazunk meg tetraéderek egyensúlyi osztályozó mátrixaira vonatkozóan. A tetraéderek 5 dimenziós konfigurációs terére illesztett ortogonális háló csúcsaiban elhelyezkedő 760000 darab tetraéder numerikus vizsgálata alapján kevesebb, mint 300 egyensúlyi mátrixot sikerült azonosítani a kombinatorikailag lehetséges 2^16=65536 mátrix közül. Jelen dolgozatban ugyan nem igazoljuk, hogy több mátrix nem létezhet, de megfogalmazunk olyan elveket, melyekkel egyes mátrixok létezését ki lehet zárni. Külön hangsúlyt fektetünk a monostabil és monoinstabil tetraéderek egyensúlyi osztályozó mátrixaira, és párhuzamot vonunk a homogén tetraéderek egyensúlyi osztályozó mátrixaival is.

Irodalomjegyzék:

[1] Középiskolai matematikai és fizikai lapok, 70. ´évfolyam 5. szám, Domokos Gábor, Kovács Flórián, Lángi Zsolt, Regős Krisztina, Varga Péter Tamás: Konvex poliéderek egyensúlyai

[2] :V.I. Arnold, Ordinary differential equations 10th printing, 1998. MIT Press.

[3] Várkonyi, Péter & Domokos, Gabor. (2006). Mono-monostatic bodies. The Mathematical Intelligencer. 28. 34-38. 10.1007/BF02984701.

[4] Regős Krisztina: Piramisok geometriája. 2018. Tudományos Diákköri Konferencia

[5] Tim Poston – Ian Stewart: Catastrophe Theory and Its Applications. Courier Corporation, 1996 048669271X, 9780486692715

[6] Marschner, S. and Shirley, P. (2018) Fundamentals of Computer Graphics. 4th edn. CRC Press, Chapter 2, Section 7.

szerző

• 
  Almádi Gergő
  Építészmérnöki mesterképzési szak osztatlan
  egységes, osztatlan képzés

konzulensek

• 
  Dr. Domokos Gábor
  egyetemi tanár, Morfológia és Geometriai Modellezés Tanszék
• 
  Regős Krisztina
  doktorandusz, Morfológia és Geometriai Modellezés Tanszék