N-oldalú Bézier felületek alkalmazása a számítógéppel segített tervezésben
Az általános topológiájú szabadformájú objektumok modellezése a számítógéppel segített tervezés egy fontos területe. Szabadformájú felületeket nem tudunk modellezni egyszerű implicit formában adott felületekkel (síkok, hengerek), meghatározásukhoz paraméteres tenzorszorzat felületeket szoktak használni. Egy jól ismert módszer, hogy kontrollpoliéderek segítségével indirekt módon hozunk létre komplex szabadformájú objektumokat. Az egyik legelterjedtebb módszer a rekurzív felosztásos eljárások családja, mely hatalmas szakirodalommal rendelkezik a klasszikus Doo‒Sabin- és Catmull‒Clark-féle felosztástól a legújabb modellezési technikákig[1]. Ezen módszerek egymásba ágyazott poliédersorozatokat generálnak, melyek tartanak egy sima határfelülethez, azaz approximatív reprezentációk.
Dolgozatomban egy alternatív felületreprezentációval foglalkozom, amely explicit módon származtatható a kontrollpoliéderből; nem approximatív, hanem folytonos reprezentáció, így a felület jellemzőit és a felületi áthatásokat közvetlenül meg lehet határozni. A kontrollpoliéderből szabadformájú görbehálókat származtatok, ezeket a görbéket interpolálják a felületet alkotó patchek. Két lehetséges algoritmust vizsgáltam: az első esetben a görbeháló topológiája megegyezik a kontrollpoliéderrel, míg a másodikban egy duális gráfot alkot. Mindkét esetben a patchek oldalainak száma függ a kontrollpoliéder lapjainak, illetve egy csúcsába összefutó éleinek számától, azaz nem kizárólag négyoldalú felületeket kapunk.
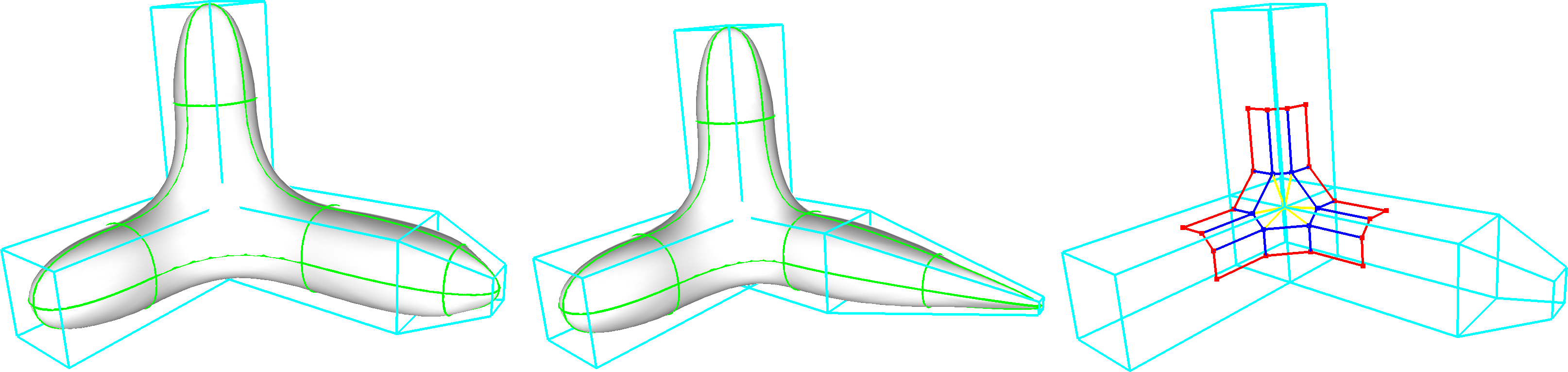
A szakirodalomban fellelhető klasszikus parametrikus felületreprezentációk négy oldalú doménnel és szabályos rácsba rendezett kontrollstruktúrával dolgoznak. Ezzel szemben a kutatásomban egy speciális felületkonstrukciót, az általánosított Bézier-patchet[2] használtam, amely n-oldalú poligonális domént és n-oldalú kontrollstruktúrát használ. Algoritmusokat fejlesztettem ki a fenti modellezési technikák megvalósítására; első lépésben görbehálót hozunk létre a kontrollpoliéder alapján, biztosítva a közös érintő síkokat a csúcsokban, majd szabályozzuk a görbe teltségét. Ezután meghatározzuk az n-oldalú felület belső kontrollpontjait úgy, hogy az oldalak mentén végig biztosítva legyen a közös érintő sík, és ezáltal a folytonosság. Ehhez a twist kontrollpontok megfelelő beállítása szükséges, mely technikai megoldása az ún. irányblend alkalmazása.
Az algoritmus működésének igazolására egy 3D-s programot fejlesztettem ki, amely egy adott kontrollpoliéder alapján előállítja a Bézier-patchek kontrollpontjait oly módon, hogy azok simán összekapcsolódva egy komplex felületet alkossanak. Lehetőség van a konstrukció alapját képező geometriai jellemzők megjelenítésére. Különböző grafikus felületminőség indikátorokkal lehet követni a kontrollpoliéder interaktív módosításával történő felület változásokat.
[1] Jörg Peters: Splines for Meshes with Irregularities
The SMAI Journal of Computational Mathematics, Volume S5, pp. 161-183, (2019)
[2] T. Várady, P. Salvi, G. Karikó: A Multi-sided Bézier Patch with a Simple Control Structure
Compter Graphics Forum 35: 2 pp. 307-317, (2016)
szerző
-
Szörfi Jázmin
Mérnök informatikus szak, mesterképzés
mesterképzés (MA/MSc)

